Cellular Automata Experiment: 01

Intialize

Defines System Name for file export later

In[32]:=

Import raster image, get RGB vector list and stripping the Mathematica Graphics data.

In[141]:=

Acceleration Field

Wrap vectors in function named 'vector' so it will work with the Cellular Automata function.  The Cellular Automata function utilizes a ListCorrelate while workings and the vector list causes errors.  Later this 'vector' function will return the vector list unchanged.

In[36]:=

Acceleration
The Acceleration function takes a 2D list of symbols represeting 3D vectors and outputs a new symbol of the sum of the cross products of the vectors in the Von Neuman neighborhood times the time enveloped by a Sin curve.  This will give an every increasing magintude to the acceleration that will increase in cycles.

In[37]:=

Define the intial conditions of the Cellular Automata inculding the number of time steps.

In[38]:=

Run the Cellular Automat

In[41]:=

Velocity Field

Velocity
Takes the acceleration field and a 2D list of 3D vectors as the initial velocity and compiles a velocity field at each time step by adding the acceleration at that time step to the previous time step's velocity.

In[42]:=

Produce still initial velocity and calculate velocity field.

In[43]:=

Surfaces

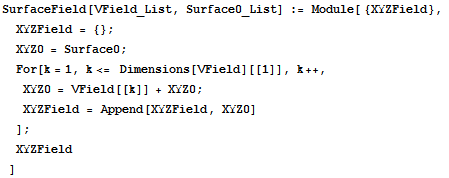
SurfaceField
Similiar to the Velocity function.  Given the velocity field and a 2D list of 3D vectors as the positions of the vertices of the surface, the function compiles a series of coordinates at each time step by moving each point by the velocity of that point at each time step.

In[45]:=

In[46]:=

Visualization

In[53]:=

Plots of X axis coordinates

In[54]:=

Plots of Y axis coordinates

In[50]:=

Plots of Z axis coordinates

In[51]:=

Velocity vectors at points on transformed surfaces.

In[55]:=

Out[55]=

Output Surfaces

melEncoding
Requires a 2D List of 3D vectors and integer number for labeling purposes.  Begin formatting array of vectors for export by converting to a string and replacing ','s with a space.  Initialize counters.  'i' for CV's in u direction. 'j' for CV's in v direction. 'd' gives size of image.  Then move through lists and replace characters with mel code to select the surface and move the CV according to the SurfaceArray vectors.  Finally add mel code header that creates the nurbs suface.  Return String of mel code that creates nurbsPlane and moves CV's to locations in 2D list.

In[57]:=

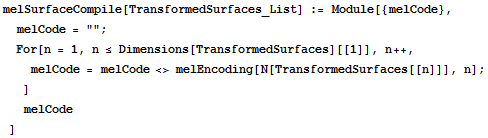
melSurfaceCompile
Takes the list of surface coordinates and produces one surface at each time step.

In[58]:=

In[71]:=

Export strings into .mel file.

In[72]:=

Out[72]=

In[56]:=

Out[56]=

Created by Mathematica  (October 23, 2006)